
오늘 한 일은,
- SQL 공부
- [코드카타] 3문제 풀기 (107~109번)
- 파이썬 공부
- [파이썬 문제풀이] 기초 관통 실습 풀기
- [머신러닝 소프트랜딩] 수강하기
- [기초 통계학] 2주차 수강하기
- [수준별 학습반 - standard] OT 수강하기
SQL 공부: [코드카타] SQL 문제 풀기 (107~109번)
107. (1789) Primary Department for Each Employee
Employees can belong to multiple departments. When the employee joins other departments, they need to decide which department is their primary department.
Note that when an employee belongs to only one department, their primary column is'N'.
Write a solution to report all the employees with their primary department. For employees who belong to one department, report their only department.
Return the result table in any order.
-- 제출한 쿼리(정답 처리됨, 그러나 시간이 많이 걸린 편에 속함)
SELECT employee_id,
department_id
FROM Employee
GROUP BY employee_id
HAVING COUNT(DISTINCT department_id) = 1
UNION
SELECT employee_id,
department_id
FROM Employee
WHERE primary_flag = 'Y'
이번에 쿼리는 별로 크게 머리를 쓰지 않고
- ① department_id가 하나인 직원들의 employee_id와 department_id를 구하고
- ② primary_flag가 'Y'인 행에서 employee_id와 department_id를 구해서
- ③ ①과 ②를 UNION으로 합침
이렇게 작성했다.
통과는 됐는데 시간이 많이 걸린 축에 속했다.


가장 많이 조회된 쿼리는 내가 작성한 내용을 WHERE절에 OR 연산자로 작성한 것이었다. 같은 내용인데 시간이 훨씬 줄었다. UNION을 함부로 남발하지 말아야겠다...
108. (610)Triangle Judgement
Report for every three line segments whether they can form a triangle.
Return the result table in any order.
삼각형 성립 조건: 두 변의 합이 나머지 변보다 길어야 한다
-- 정답 처리 됨
SELECT *,
CASE WHEN (x+y > z) AND (y+z > x) AND (x+z > y) THEN 'Yes' ELSE 'No' END triangle
FROM Triangle
109. (180) Consecutive Numbers
Find all numbers that appear at least three times consecutively.
Return the result table in any order.
연달아.....? WHERE절에 윈도우 함수를 사용할 수 있는 건가..? 안 될 텐데...
-- 제출한 쿼리 (정답 처리됨)
SELECT DISTINCT s.num ConsecutiveNums
FROM (
SELECT *,
LAG(num, 1, NULL) OVER (ORDER BY id) num_prev1,
LAG(num, 2, NULL) OVER (ORDER BY id) num_prev2
FROM Logs
) s
WHERE (s.num = s.num_prev1) AND
(s.num = s.num_prev2)
이전에 풀었던 SQL 코드카타 문제 중에 LAG() OVER를 사용했던 쿼리가 생각났다.
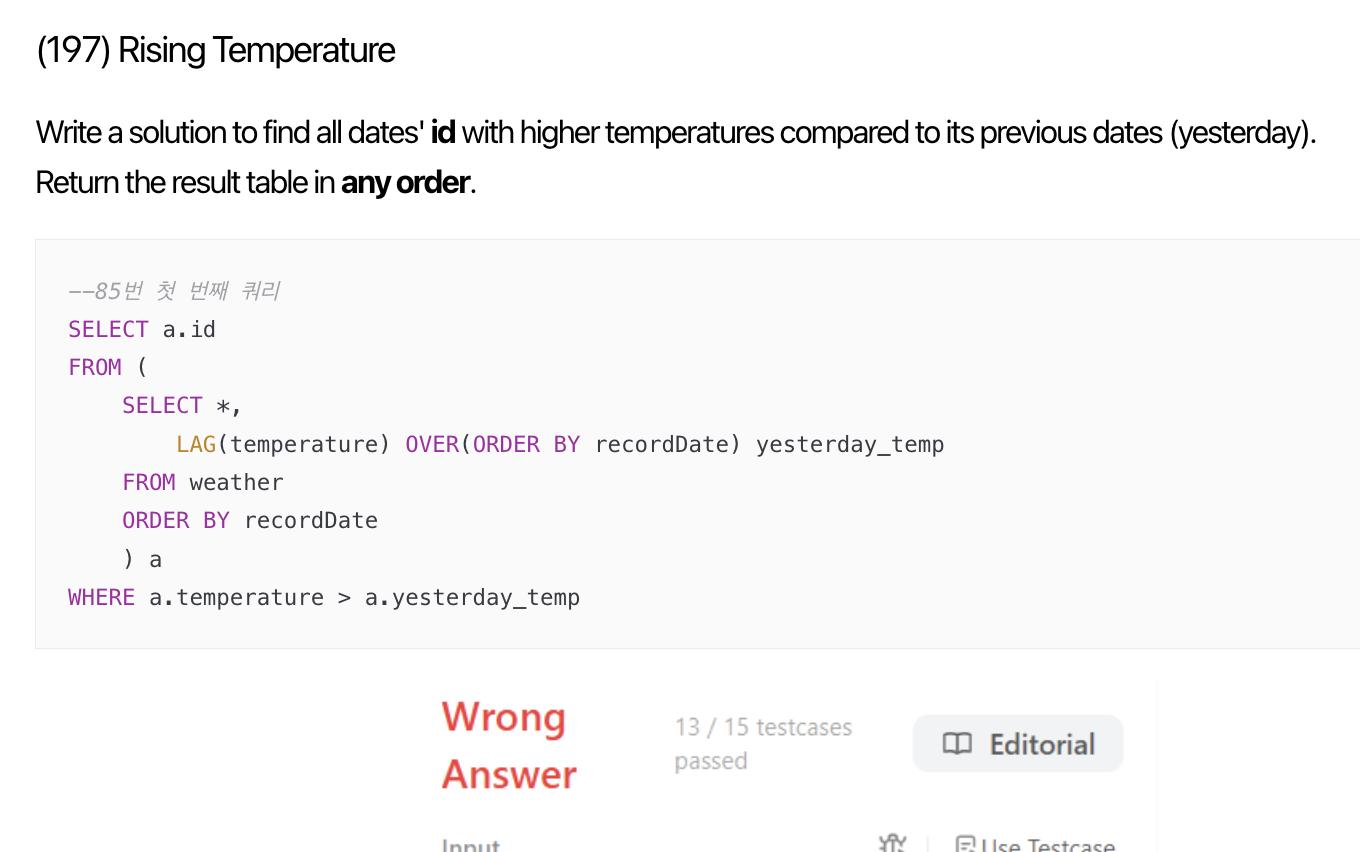
그래서 그 기억으로 한 행 전의 num을 보여주는 컬럼, 두 행 전의 num을 보여주는 컬럼을 LAG() 함수로 사용해서 만들어 3개의 행이 일치하는 숫자를 조회하면 어떨까 싶었다. 그렇지만 어떻게 LAG() OVER를 써야 하는지 기억이 안 나서 우선 문법부터 찾아봤다.
[참고] [MSSQL] LAG, LEAD 함수를 이용한 이전행, 다음행 조회 방법 지금 보니 mssql이었네....
- LAG(컬럼명, n, 기본값) OVER (PARTITION BY … ORDER BY…)
- 컬럼명에 기입한 컬럼을 n행 이전의 값을 조회함
- 해당 컬럼의 현재 행 기준에서 n행 이전의 값이 없다면 설정한 기본값으로 채움
LAG() 함수를 이용해 서브쿼리 s를 짜놓고 그를 인라인뷰로 사용해서 WHERE절로 1행 전의 num과 일치하고 또 2행 전의 num과도 일치하는 num을 조회하도록 작성했다.
통계학 공부: [기초 통계학] 2주차 수강하기
모집단과 표본
모집단(population)
- 관심이 대상이 되는 전체 집단
- 전수조사 : 모집단 전체를 조사하는 방법. 대규모일 경우 비용과 시간이 많이 투입됨.
표본(sample)
- 모집단에서 추출한 일부
- 표본조사 : 표본만을 조사하는 방법. 시간과 비용이 적게 들지만 표본이 대표성을 갖고 있어야 함.
- 🔎표본을 사용하는 이유
- [비용과 시간 측면] 비용과 시간을 절약하기 위해
- [접근성 측면] 모든 데이터를 수집하는 것이 불가능하기에
- [표본의 대표성 측면]
무작위로 표본을 추출해 편향을 최소화하면 모집단의 다양한 특성을 포함할 수 있기에 해당 결과를 모집단 전체에 일반화할 수 있음 - [데이터 처리의 용이성 측면]
전체 데이터를 다루는 것보다 표본 데이터만을 다루는 것이 데이터 처리 및 분석에 훨씬 용이함 - [데이터 품질 관리 측면]
상대적으로 크기가 작은 표본에선 데이터 품질을 관리하기 쉽고, 오류 및 이상값을 식별하고 발견하기도 좋음 - [모델 검증의 용이성 측면] 통계적 모델이 표본에 잘 맞는다면 모집단에도 적합할 가능성이 높음
- 표본조사의 예시
- 도시 연구: "한 도시의 모든 가구 중 100가구를 조사해 평균 전력 사용량을 추정"
- 의료 연구: "특정 치료법의 효과를 알아보기 위해 해당 질병을 가진 전체 환자 중 표본을 통해 이를 조사"
- 시장 조사: "소비자 선호도를 파악하기 위해 전체 소비자 중 표본을 추출해 전체 시장의 트렌드를 추정"
- 정치 여론 조사: "선거 전 여론 조사를 통해 전체 유권자의 투표 경향을 추정해 선거 결과를 예측"
- 🔎표본을 사용하는 이유
파이썬 실습: 히스토그램으로 모집단과 표본 비교해보기
import numpy as np
import matplotlib.pyplot as plt
# 모집단 생성 (예: 국가의 모든 성인의 키 데이터)
population = np.random.normal(170, 10, 1000)
# 표본 추출
sample = np.random.choice(population, 100)
plt.hist(population, bins=50, alpha=0.5, label='population', color='blue')
plt.hist(sample, bins=50, alpha=0.5, label='sample', color='red')
plt.legend()
plt.title('population and sample distribution')
plt.show()
- numpy.random() 모듈: 다양한 확률 분포에 따라 난수를 생성하는 기능
- np.random.normal(loc, scale, size) : 정규분포를 따르는 난수를 생성함
- 정규분포: 평균과 표준편차를 중심으로 데이터가 대칭으로 분포
- loc(float): 정규분포의 평균
- scale(float): 정규분포의 표준편차
- size(int / tuple of ints): 출력 배열의 크기 정수 하나 넣으면 1차원 배열, 튜플로 넣으면 2차원 이상도 가능
- np.random.choice(a, size, replace, p) : 주어진 배열에서 임의로 표본을 추출함
- a: 표본을 추출할 모집단
- size(int / tuple of ints): 출력 배열의 크기
- replace(boolean): 표본 추출할 때 중복으로 선택할지(True), 중복 없이 선택할지(False) [기본은 True]
- p: 각 요소가 선택될 확률. 해당 배열의 합은 1이어야 함.
- np.random.normal(loc, scale, size) : 정규분포를 따르는 난수를 생성함
- matplotlib.pyplot.hist(): 데이터의 분포를 시각화하는 데 유용한 히스토그램을 그림
- plt.hist(bins, alpha, label, color)
- bins(int / list): 데이터를 몇 개의 구간으로 나눌지. (정수는 개수, 리스트는 값의 경계를 직접 지정함)
- alpha: 막대의 투명도 0~1 사이의 값을 입력하는데 0으로 갈수록 투명해짐.
- label: 이름을 지정하는데 여러 히스토그램을 그릴 때 범례로 추가됨
- color: 막대의 색상
- plt.hist(bins, alpha, label, color)
표본 오차와 신뢰 구간
표본 오차(Sampling Error)
- 표본에서 계산한 통계량과 모집단의 진짜 값 간의 차이
- 표본이 모집단을 완벽하게 대표할 순 없기에 발생할 수밖에 없지만, 표본의 크기와 표본 추출 방법에 따라 표본 오차가 달라짐
- [표본의 크기] 표본의 크기가 커질수록 표본 오차는 줄어듦
- = 더 많은 표본 데이터를 수집할수록 모집단을 더 잘 대표하게 됨
- [표본 추출 방법] 무작위로 표본을 추출해 모든 모집단의 요소가 선택될 동등한 기회를 갖게 해야 함
신뢰 구간(Confidence Interval)
- 모집단의 특정 파라미터(평균, 비율 등)에 대해서 추정한 값이 포함될 것으로 기대하는 범위
모집단의 평균이나 비율이 어디부터 어디까지 중에는 있을 것이다~ - 신뢰구간 계산 방법 : (표본 평균) ± z*(표준 오차)
- z: 선택한 신뢰 수준에 해당하는 값 (95% 신뢰 수준을 선택하면 z는 1.96)
- 일반적으로 95% 신뢰 수준을 많이 사용함
파이썬 실습: SciPy 라이브러리로 신뢰 구간 구하기
import scipy.stats as stats
# 표본 평균과 표본 표준편차 계산
sample_mean = np.mean(sample)
sample_std = np.std(sample)
# 95% 신뢰구간 계산
conf_interval = stats.t.interval(0.95, len(sample)-1, loc=sample_mean, scale=sample_std/np.sqrt(len(sample)))
print(f"표본 평균: {sample_mean}")
print(f"95% 신뢰구간: {conf_interval}")
- scipy.stats : 통계 분석을 위한 다양한 함수와 클래스들을 제공하는 모듈
- stats.t.interval(alpha, df, loc, scale) : 주어진 신뢰 수준(alpha)에서 t-분포를 사용해 신뢰 구간을 계산함
- alpha: 신뢰 수준 (95% 신뢰 구간을 원하면 alpha는 0.95)
- df: 자유도, 일반적으로 표본의 크기에서 1을 뺀 값으로 설정
- loc: 위치, 일반적으로 표본 평균으로 설정
- scale: 일반적으로 표본 표준 오차로 설정 (표본 표준 오차: 표본의 표준편차를 표본 크기의 제곱근으로 나눔)
분포
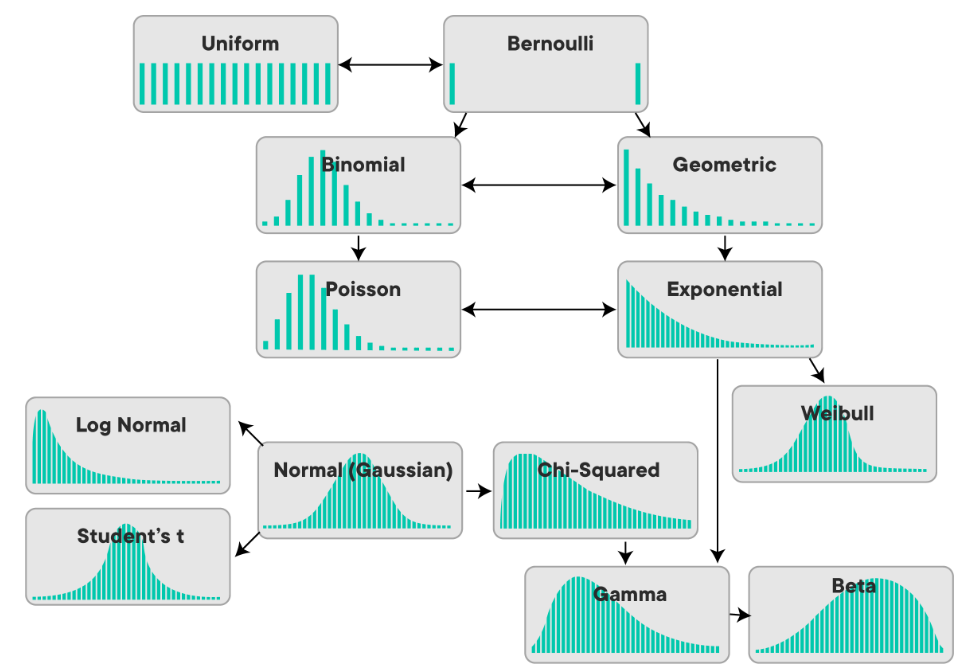
① 정규 분포
- 종 모양의 대칭 분포
- 대부분의 데이터가 평균 주위에 몰려 있음
- 평균에서 멀어질수록 데이터의 빈도가 감소
- 표준편차는 분포의 퍼짐 정도를 나타냄 표준편차가 크면 평균에서 많이 퍼져있고, 작으면 평균에 주로 몰려있음
- 데이터의 수가 많을수록 대부분 정규분포를 따름 (cf. 중심 극한 정리)
물론 데이터 수가 적은 경우 혹은 많아도 따르지 않는 경우가 존재하기에 그땐 다른 분포를 사용해야 함
# 정규분포 생성
normal_dist = np.random.normal(170, 10, 1000)
# 히스토그램으로 시각화
plt.hist(normal_dist, bins=30, density=True, alpha=0.6, color='g')
# 정규분포 곡선 추가
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, 170, 10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('normal distribution histogram')
plt.show()
② 긴 꼬리 분포
- 대부분의 데이터가 분포의 한쪽 끝에 몰려 있고, 반대쪽으로 긴 꼬리가 이어지는 형태의 분포
소수가 엄청난 영향력을 발휘하는 경우 - 정규분포와 달리 비대칭적임 아무리 데이터가 많아져도 정규분포가 되지 않음
- 특정한 하나의 분포를 의미하지 않으며 여러 종류의 분포(예: 파레토 분포, 지프의 법칙, 멱함수)를 포함
이 중 파레토 분포가 경제학에서 자주 사용하는 분포라 함 - 대표적으로 사용한 예시
- 소득 분포 (일부 부유층이 전체 소득에서 큰 비중을 차지하는 소득 분포)
- 온라인 쇼핑 (대형 온라인 쇼핑몰에서는 소수의 인기 제품이 많이 팔리고, 많은 수의 비인기 제품들은 적게 팔림)
- 도서 판매 (소수의 베스트셀러 도서가 전체 판매량의 대부분을 차지하고, 많은 수의 비인기 도서들은 적게 팔림)
# 긴 꼬리 분포 생성 (예: 소득 데이터)
long_tail = np.random.exponential(1, 1000)
# 히스토그램으로 시각화
plt.hist(long_tail, bins=30, density=True, alpha=0.6, color='b')
plt.title('long tail distribution histogram')
plt.show()
③ 스튜던트 t 분포
- 모집단의 표준편차를 알 수 없고 표본의 크기가 작은 경우(일반적으로 30미만)에 사용되는 분포
- 정규분포와 유사하지만, 표본의 크기가 작을수록 꼬리가 두꺼워지는 특징
- 자유도가 커질수록 정규분포에 가까워짐 *자유도: 표본의 크기와 관련 있는 값
- 대표적으로 사용한 예시
- 작은 표본의 평균을 비교할 때
- 약물 시험: 새로운 약물의 효과를 테스트할 때, 소규모 임상 시험에서 두 그룹 간의 차이를 분석하는 데 사용
# 스튜던트 t 분포 생성
t_dist = np.random.standard_t(df=10, size=1000)
# 히스토그램으로 시각화
plt.hist(t_dist, bins=30, density=True, alpha=0.6, color='r')
# 스튜던트 t 분포 곡선 추가
x = np.linspace(-4, 4, 100)
p = stats.t.pdf(x, df=10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('student t distribution histogram')
plt.show()
④ 카이제곱 분포
- 범주형 데이터의 독립성 검정이나 적합도 검정에 사용하는 분포
- 독립성 검정 : 두 범주형 변수 간 관계가 있는지를 확인할 때 사용
성별과 직업 선택 간에 관계가 있는가?
성별이 후보 지지율에 영향을 미치는가? - 적합도 검정 : 관측한 값들이 특정 분포에 해당하는지를 검정할 때 사용
주사위의 각 면이 동일한 확률로 나오는가?
노란색 완두콩과 연두색 완두통이 멘델의 유전 법칙에 따라 3:1의 비율로 나타나는가?
- 독립성 검정 : 두 범주형 변수 간 관계가 있는지를 확인할 때 사용
- 상관관계나 인과관계를 판별하고자 하는 원인의 독립변수가 ‘완벽하게 서로 다른 질적 자료’일 때 활용
- 자유도에 따라 모양이 달라짐
- 데이터의 값이 많아질수록 카이제곱 분포도 정규분포에 가까워짐
# 카이제곱분포 생성
chi2_dist = np.random.chisquare(df=2, size=1000)
# 히스토그램으로 시각화
plt.hist(chi2_dist, bins=30, density=True, alpha=0.6, color='m')
# 카이제곱분포 곡선 추가
x = np.linspace(0, 10, 100)
p = stats.chi2.pdf(x, df=2)
plt.plot(x, p, 'k', linewidth=2)
plt.title('카이제곱 분포 히스토그램')
plt.show()
⑤ 이항 분포
- 두 가지 결과만을 가지는 실험을 여러 번 반복했을 때 성공 횟수의 분포
- 연속된 값을 가지지 않고, 특정한 정수 값만을 가지기에 연속적으로 그려지지 않음
동전을 10번 던질 때 앞면이 나오는 횟수는 0, 1, 2, ..., 10과 같은 정수 - 이산형 분포라고 지칭하기도 함
- 대표적으로 사용한 예시
- 동전 던지기 : 동전을 10번 던졌을 때, 앞면이 나오는 횟수
- 품질 관리 : 제조업체가 제품의 불량률을 모니터링할 때, 무작위로 선택된 100개의 제품 중 불량품의 수
# 이항분포 생성 (예: 동전 던지기 10번 중 앞면이 나오는 횟수)
binom_dist = np.random.binomial(n=10, p=0.5, size=1000)
# 히스토그램으로 시각화
plt.hist(binom_dist, bins=10, density=True, alpha=0.6, color='y')
plt.title('이항 분포 히스토그램')
plt.show()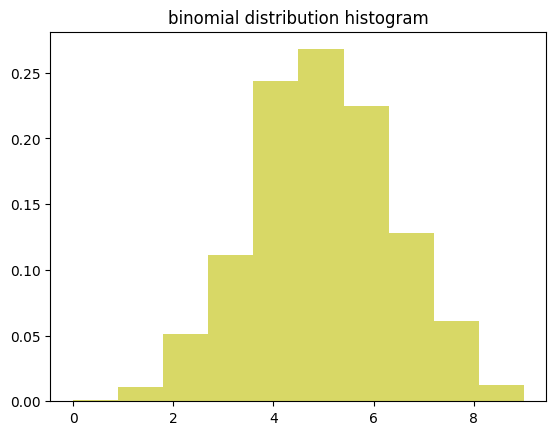
⑥ 푸아송 분포
- 단위 시간 또는 단위 면적 당 발생하는 사건의 수를 모델링할 때 사용하는 분포
- 평균 발생률(λ)를 가진 사건이 주어진 시간 또는 공간 내에서 몇 번 발생하는지를 나타냄
- 평균 발생률(λ): 주어진 시간이나 공간에서 사건이 몇 번 발생했는지
- 단위 시간 또는 단위 면적당 희귀하게 발생하는 사건의 수를 모델링하는 데 적합
- 연속된 값을 가지지 않기 때문에 푸아송 분포도 역시 이산형 분포에 해당
- 평균 발생률 λ가 충분히 크다면 정규분포에 근사
- 대표적으로 사용한 예시
- 콜센터: 특정 시간 동안 콜센터에 도착하는 전화 통화의 수
- 교통 사고: 특정 도로 구간에서 일정 기간 동안 발생하는 교통사고의 수
- 문자 메시지: 특정 시간 동안 수신되는 문자 메시지의 수
- 웹사이트 트래픽: 특정 시간 동안 웹사이트에 도착하는 방문자의 수
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# 푸아송 분포 파라미터 설정
lambda_value = 4 # 평균 발생률
x = np.arange(0, 15) # 사건 발생 횟수 범위
# 푸아송 분포 확률 질량 함수 계산
poisson_pmf = poisson.pmf(x, lambda_value)
# 그래프 그리기
plt.figure(figsize=(10, 6))
plt.bar(x, poisson_pmf, alpha=0.6, color='b', label=f'Poisson PMF (lambda={lambda_value})')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.title('Poisson Distribution')
plt.legend()
plt.grid(True)
plt.show()
분포 정리하기
분포 선택 시 참고할 내용
- 데이터 수가 충분히 많다 → 무조건 정규분포
- 데이터 수가 작다 → 스튜던트 t 분포
- 일부 데이터가 전체적으로 큰 영향을 미친다 → 롱 테일 분포(그 중에서도 파레토 분포)
- 범주형 데이터의 독립성이나 적합도 검정 → 카이제곱 분포
- 결과가 2개만 나오는 상황이다 → 이항 분포
- 특정 시간이나 특정 공간에서 발생하는 사건에 대한 것이다 → 푸아송 분포
'[내배캠] 데이터분석 6기 > 본캠프 기록' 카테고리의 다른 글
| [본캠프 33일차] SQL 공부, 파이썬 공부, 통계학 공부, 아티클 스터디② (0) | 2025.04.03 |
|---|---|
| [본캠프 32일차] SQL 공부, 통계학 공부, 알고리즘 공부, 아티클 스터디① (0) | 2025.04.02 |
| [본캠프 30일차] chap 3의 시작, SQL 공부, 파이썬 공부 (0) | 2025.03.31 |
| [본캠프 29일차] 기초 프로젝트 발표 (0) | 2025.03.28 |
| [본캠프 28일차] SQL 코드카타, 파이썬 코드카타, 기초 프로젝트 준비⑥ (0) | 2025.03.27 |